Appendix B Perspectives
¶In this appendix we draw attention to the many ways in which a single idea can be viewed from multiple perspectives.
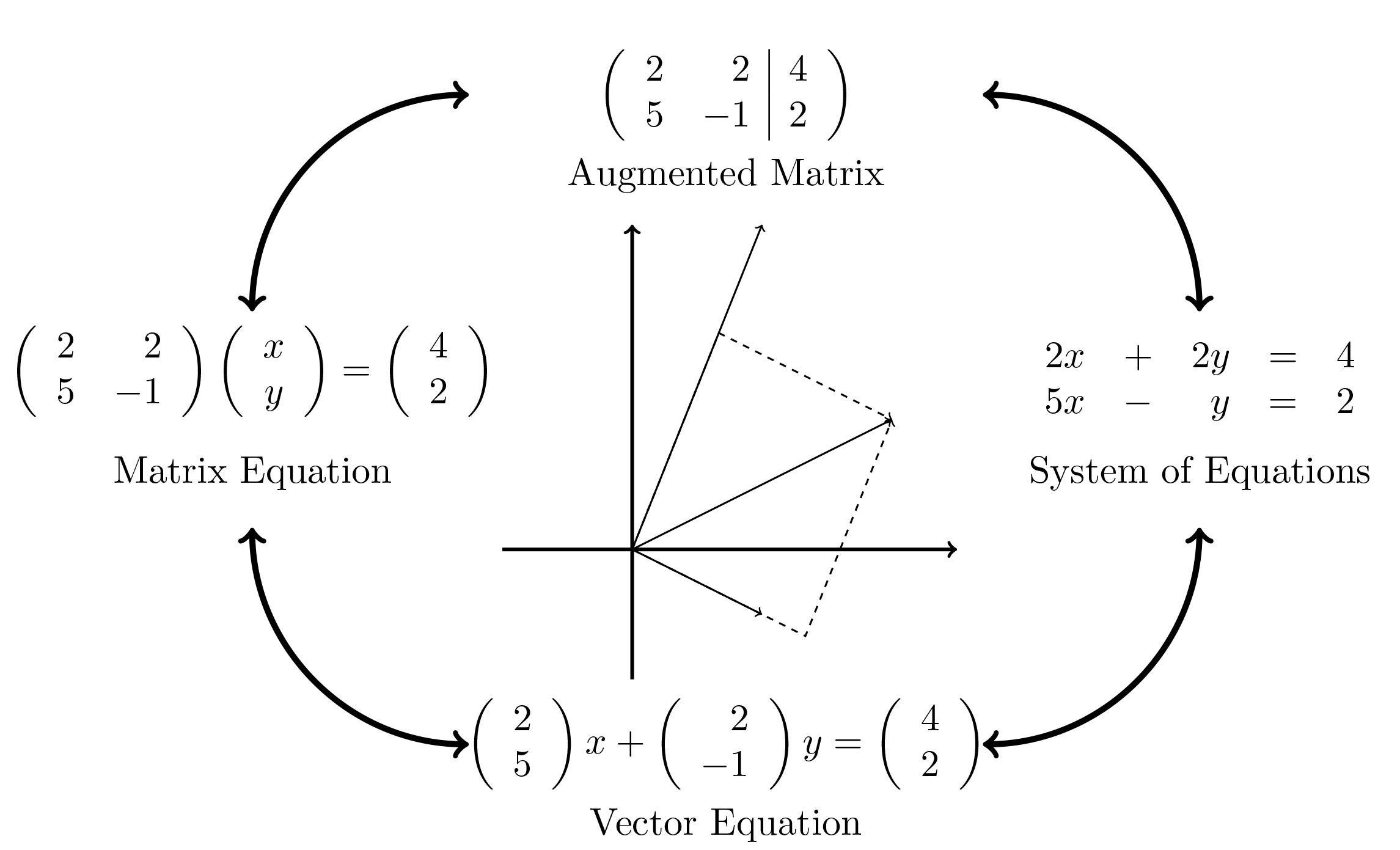
Given an \(m\times n\) matrix \(A\text{,}\) with columns \(A_j,\ j=1,\ldots,n\text{,}\) and vectors \(\vec{b}\in \mathbb{R^m}\) and \(\vec{x}\in \mathbb{R^n}\) we get the following equivalences:
The Linear System |
Given the Set of Vectors |
The Matrix Equation |
Given the Linear Transformation |
|
\(\left(\sum_{j=1}^{n} a_{ij}x_i\right)=b_i\) is |
\(\mathcal{B}_A=\left\{A_j\right\}_{j=1}^n\) |
\(A\vec{x}=\vec{b}\) |
\(T_A(\vec{x})=A\vec{x}\) |
Consistent for some \(\vec{b}\text{,}\) but the solution is not unique |
\(\vec{b}\in span\left(\mathcal{B}_A\right)\) |
Has infinitely many solutions |
\(\vec{b}\in Image\left(T_A\right)\) |
Consistent for some \(\vec{b}\) and the solution is unique |
They are linearly independent and \(\vec{b}\in span\left(\mathcal{B}_A\right)\) |
Has exactly one solution, \(n \lt m\text{,}\) \(A\) has a pivot in every column |
\(\vec{b}\in Image\left(T_A\right)\text{,}\) and \(T_A\) is 1-1 |
Consistent for all \(\vec{b}\text{,}\) but the solution is not unique |
\(span\left(\mathcal{B}_A\right)=\mathbb{R}^m\) |
Has infinitely many solutions, \(A\) has a pivot in every row, \(m \lt n\) |
\(Image\left(T_A\right)=\mathbb{R}^m\text{,}\) \(T_A\) is onto |
Consistent for all \(\vec{b}\) and the solution is unique |
\(\mathcal{B}_A\) is a basis for \(\mathbb{R}^m\) |
Has exactly one solution, \(A\) is invertible, \(m=n\) |
\(Image\left(T_A\right)=\mathbb{R}^m\text{,}\) \(T_A\) is 1-1 and onto |
Inconsistent |
\(\vec{b}\not\in span\left(\mathcal{B}_A\right)\) |
Has no solution |
\(\vec{b}\not\in Image\left(T_A\right)\) |