Section 3.4 Stirring Things Up
Objectives
- Falconer's Discussion of Permutations
- Falconer's Columnar Transposition
Subsection 3.4.1 Key Permutations
Sect. 2: Of Secret Writing by Altering the Places of the Letters, Where the Powers Remain the Same
Part 1: Of the Combinations of Three or More Letters
The first remarkable improvement I find of this kind of cryptography by altering the places of letters, is by the regular combinations of three, four, or more letters: I had it of a gentleman, who (I am fully satisfied) would put it to no bad use; but since it may fall of bad hands, I have his leave to provide against its harm. And that we may proceed regularly therein it is necessary, first to inquire, “how many several ways any given number of letters may be combined?” (i.e.) How many differnt positions they can regularly admit of. And for that end I have hereunto subjoined the following table:
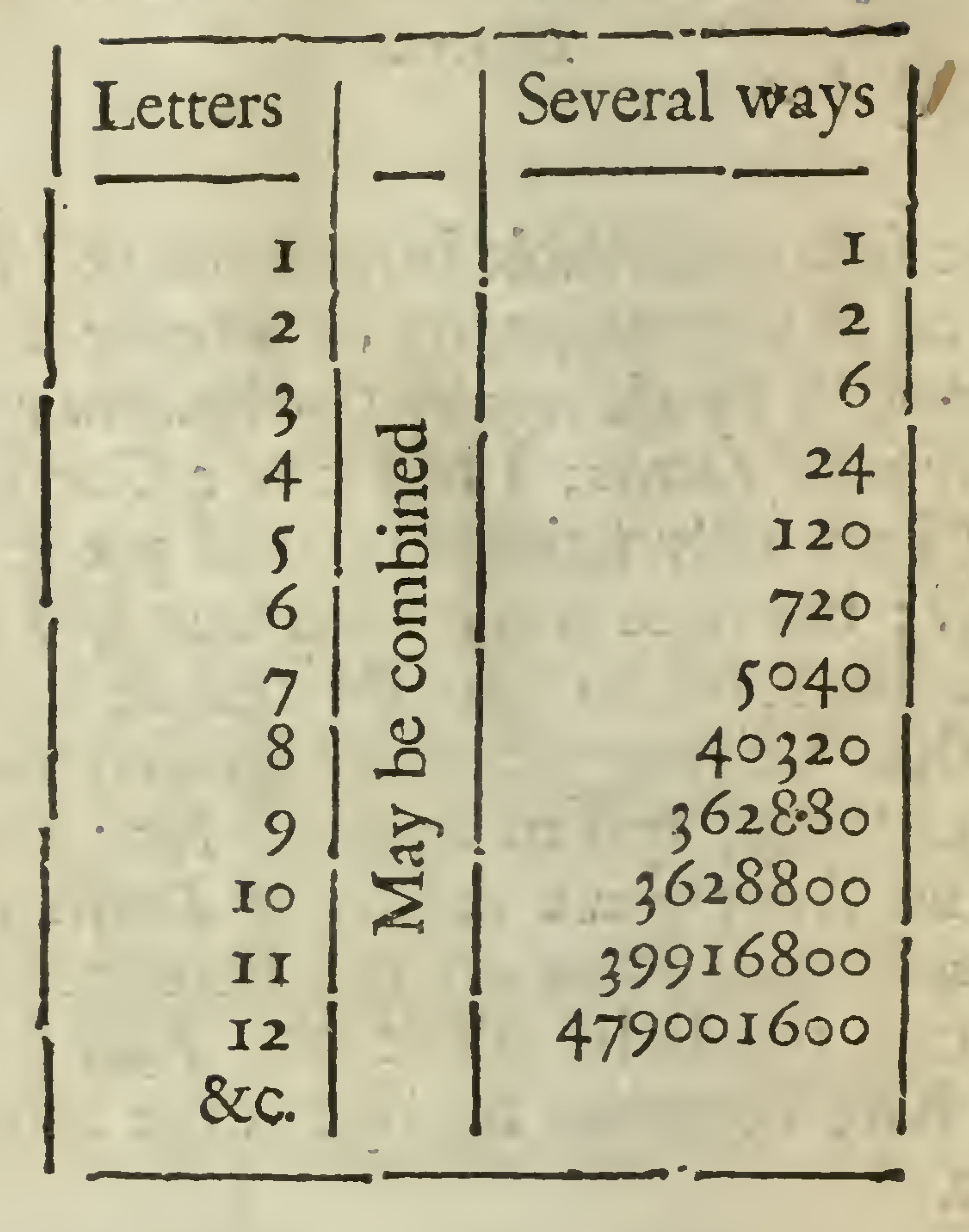
Construction of the Table.
- At the left-hand of your table stands a rank of figures expressing the number of letters to be combined, encreasing in an arithmetical proportion from unity, or 1 and by common excess of 1, or unity.
- To the right hand of these stands the number of Combinations, 1 or several ways they can be combined.
- As for 1, being it has but one positions, I set 1 opposite to it in the rank of combinations.
- I multiply 1, in the column of combinations, by two, in the column of letters, and set the product, viz. 2, opposite to it, which shows how often two letters or things can be combined, viz. two times.
- I multiply the 2 in the row of combinations, by 3 in the column of letters; and over against it I set 6 for the product, which shows that three letters have sixe regular positions or combinations.
- ...
Demonstration.
- It is manifest, that one letter or thing has but one position, and two letters have twice the position of 1, viz. once before and once after it. e.g. AB, BA.
- From the combination of two letters we find that of 3, for the new Letter added is three times applicable to the former positions, viz. in the beginning, middle, and end, e.g. the letter C being joyned with AB, the first combination may be CAB, and the second CBA. Again put C in the middle, and it yields other differences, viz. ACB, BCA. And when C is put in the lat place, you have a fifth and sixth difference, viz. ABC, BAC.
- From the combination of three letters arises that of four letters; viz. ABCD: for D can be four several times applied to each of the former six differences; e.g. in the first, second, third, and fourth or last place.
- From the twenty four combinations arising from four letters, you have that of 5; e.g. if the letter E is added, it is five times applicable to each of the former twenty four regular positions: and so for any other number in infinitum.
I have said regular positions, because any number of letters or things may be irregularly varied in their positions very much above this order; for example, AB is capable of these irregular variations, AA, AB, BA, BB; and at this rate, three letters have no less than 27 positions in all, viz. six regular (as above) and twenty one irregular positions. ... - John Falconer [4, pp. 37-40 (65-68)]
Comprehension Check:
- How many ways does Falconer state that we can rearrange the distinct letters ABCDE?
- How does Falconer arrive at that number? What does he mean when we says "if the letter E is added, it is five times applicable to each of the former twenty four regular positions"?
- Based on what Falconer says above how many ways should we be able to arrange the distinct letters ABCDEF? How would he explain that?
- When Falconer speaks of irregular variations in the last paragraph which combinations of A and B is he considering that he hadn't before?
- Why does he say that there would be 27 positions, how does he get 27 positions from 3 letters?
- How many positions would there be if you had 4 letters, or 5?
What Falconer is discussing here are the factorials we learned about earlier. (Definition 1.1.10) Factorials are related to two other ideas permutations and combinations, which we will explore later when we discuss more complicated ciphers. For now, let's see how Falconer uses these combinations of letters.
Subsection 3.4.2 Transposition
A New Method How to Write Secretly by the Art of Combinations
- To write by the method proposed, a certain number of letters are combined to lock and unlock the epistle. The differences of writing down the positions [of the letters] ... may be varied to a vast number; ...
- The order of rows is agreed upon in parting.
- The number of letters combined, which is the key, may be expressed in the epistle by some mathematical figure, as \(\scriptsize\triangle\) for three letters, \(\Box\) for 4, etc. or by some private mark.
- They [the individuals communicating] frame a rectangular table of as many columns as there are letters combined.
- The letters so combined are placed in their natural order along the top of the table.
- Having determined of how many lines the table shall consist, the order of combinations agreed upon is set down in a row in the first column towards the left hand; as you may see in the following table.
- The table being thus prepared for writing, they observe the order of the combinations, and write according to its direction.
- When they have placed one letter of every column of all the lines, they begin a new, and so go on until the writing be finished.
- And lastly, they take the letters out of the table according to their partitions, as so many barbarous words, upon paper apart and send it to the confidant. - John Falconer [4, pp. 68-72 (40-43)]
Comprehension Check:
Let's see if you can follow Falconer's directions. Below I set up Table 3.4.1 according to his description in steps (5) and (6) and used it to encipher the pangram “the quick brown fox jumps over the lazy sleeping dog.”
- Looking at Table 3.4.2 why is the the from the beginning of the sentence written backwards? (Be sure to look carefully at the letters to the left of the row when answering.)
- In the second row of the same table why is the qui from quick written in the order it is written? (Again, be sure to look carefully at the letters to the left of the row when answering.)
- In the last row we put down the n from brown and the fo from fox, why are they in the order they are in and looking at the next table (Table 3.4.3) where do we put the x from fox and why?
- How do we finish writing the rest of the message into the boxes in the table?
- Looking at the final message why is there a little triangle at the start of the message and why were the blocks of letters written in the order they were written?
- In what ways is this different from other ciphers we have looked at? (Hint: In this cipher what does cipher text E represent, or cipher text F?)
| A | B | C | ||
| 1 | CBA | \(\phantom{WRW}\) | \(\phantom{WRW}\) | \(\phantom{WRW}\) |
| 2 | CAB | \(\phantom{WRW}\) | \(\phantom{WRW}\) | \(\phantom{WRW}\) |
| 3 | ACB | \(\phantom{WRW}\) | \(\phantom{WRW}\) | \(\phantom{WRW}\) |
| 4 | BCA | \(\phantom{WRW}\) | \(\phantom{WRW}\) | \(\phantom{WRW}\) |
| 5 | BAC | \(\phantom{WRW}\) | \(\phantom{WRW}\) | \(\phantom{WRW}\) |
| A | B | C | ||
| 1 | CBA | E | H | T |
| 2 | CAB | U | I | Q |
| 3 | ACB | C | B | K |
| 4 | BCA | W | R | O |
| 5 | BAC | \(\phantom{W}\)F\(\phantom{W}\) | \(\phantom{W}\)N\(\phantom{W}\) | \(\phantom{W}\)O\(\phantom{W}\) |
| A | B | C | ||
| 1 | CBA | EUS | HJY | TXZ |
| 2 | CAB | UPE | ISE | QML |
| 3 | ACB | COP | BEN | KVI |
| 4 | BCA | WHO | RRG | OTD |
| 5 | BAC | \(\phantom{I}\)FL\(\phantom{I}\) | \(\phantom{I}\)NEG\(\phantom{I}\) | \(\phantom{I}\)OA\(\phantom{I}\) |
Final Message:
“\(\scriptsize\triangle\) EUS HJY TXZ UPE ISE QML COP BEN KVI WHO RRG OTD FL NEG OA”
Checkpoint 3.4.4.
Decipher the following message which used the same key as the one represented in Table 3.4.1:
\(\scriptsize\triangle\) WU OO NR MD A IN L T L N U R D E A
Now I'm all turned around.
First put the blocks of text into the table row by row in alphabetical order:
| A | B | C | ||
| 1 | CBA | WU | OO | NR |
| 2 | CAB | MD | A | IN |
| 3 | ACB | L | T | L |
| 4 | BCA | N | U | R |
| 5 | BAC | D | E | A |
Now read the message out character by character according to the combinations at the left:
nowimallturnedaround
Finally, we get the original message.
Now I'm all turned around.
Checkpoint 3.4.6.
Encipher the following message using the same key as the one represented in Table 3.4.1:
“As long as the world is turning and spinning, we're gonna be dizzy and we're gonna make mistakes.” - Mel Brooks
\(\scriptsize\triangle\)LSNDNE SINENM ADIBOS NUNZMB GRGZAR OTIIAL ANWYKO TNRNMK SIEAEO WNOET HGEDIS EAGWS RSNEK ODNRA LPAGE
First we break up the message into blocks of three to make it easier to work with.
ASL ONG AST HEW ORL DIS TUR NIN GAN DSP INN ING WER EGO NNA BED IZZ YAN DWE REG ONN AMA KEM IST AKE SME LBR OOK S
Then copy each character into the table using the combination keys at the side to tell us which column to put each character in.
| A | B | C | ||
| 1 | CBA | LSNDNE | SINENM | ADIBOS |
| 2 | CAB | NUNZMB | GRGZAR | OTIIAL |
| 3 | ACB | ANWYKO | TNRNMK | SIEAEO |
| 4 | BCA | WNOET | HGEDIS | EAGWS |
| 5 | BAC | RSNEK | ODNRA | LPAGE |
Finally, we read the message out of the table from left to right and from top to bottom.
\(\scriptsize\triangle\)LSNDNE SINENM ADIBOS NUNZMB GRGZAR OTIIAL ANWYKO TNRNMK SIEAEO WNOET HGEDIS EAGWS RSNEK ODNRA LPAGE
Checkpoint 3.4.8.
Encipher the following message using the three letters as before, but with the row keys ACB - CAB - BAC - ABC, Table C.0.11 is a blank table you can copy if you need to:
“A person who never made a mistake never tried anything new.” - Albert Einstein
\(\scriptsize\triangle\)AVADAI ERENB PEKALN SAETR ODVHT RMNYE WARNI NEEIE HMTGN OIRNS NSIET ETEWE
First we break up the message into blocks of three to make it easier to work with.
APE RSO NWH ONE VER MAD EAM IST AKE NEV ERT RIE DAN YTH ING NEW ALB ERT EIN STE IN
Then copy each character into the table using the combination keys at the side to tell us which column to put each character in.
| A | B | C | ||
| 1 | ACB | AVADAI | ERENB | PEKALN |
| 2 | CAB | SAETR | ODVHT | RMNYE |
| 3 | BAC | WARNI | NEEIE | HMTGN |
| 4 | ABC | OIRNS | NSIET | ETEWE |
Finally, we read the message out of the table from left to right and from top to bottom.
\(\scriptsize\triangle\)AVADAI ERENB PEKALN SAETR ODVHT RMNYE WARNI NEEIE HMTGN OIRNS NSIET ETEWE