Skip to main content

Appendix C Blank Tables, Charts, and Images

Table C.0.1. Monoalphabetic Substitution Table
plain a b c d e f g h i
CIPHER
plain j k l m n o p q r
CIPHER
plain s t u v w x y z
CIPHER
Table C.0.2. A Numerical Alphabet
1 2 3 4 5 6 7 8 9
a b c d e f g h i
10 20 30 40 50 60 70 80 90
j k l m n o p q r
100 200 300 400 500 600 700 800 900
s t u v w x y z
This is a blank set of axes which we can use to map frequencies when performing frequency analysis.
svgpngpdf
Figure C.0.3. Axes for Mapping Letter Frequencies
You can use these blank tables when doing frequency counts.
svgpngpdf
Figure C.0.4. Blank Tables for Frequency Counts
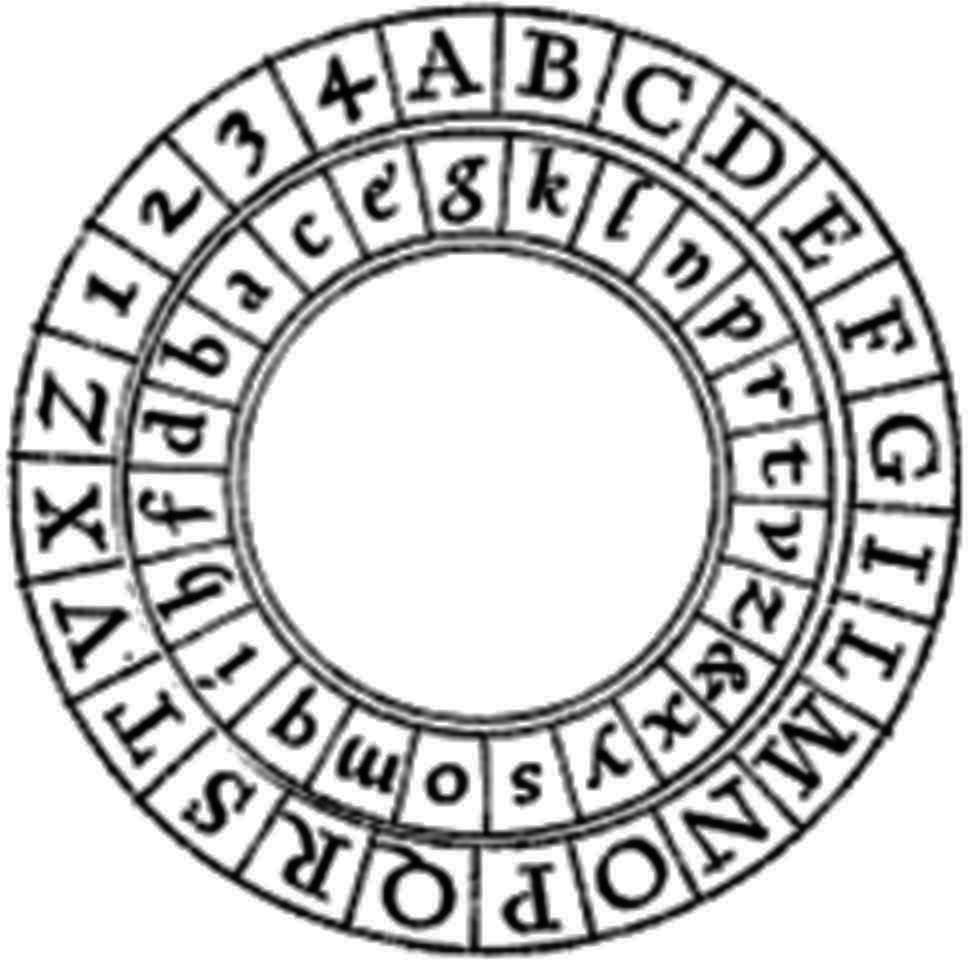
This is an image of Leon Battista Alberti's Cipher Disk as he described it.
svgpngpdf
Figure C.0.5. Alberti's Cipher Disk or “Formula”
This is an image of modern version of Alberti's Cipher Disk.
svgpngpdf
Figure C.0.6. Modern Cipher Disk or “Formula”
This is a copy of Vigenère's Table.
svgpngpdf
Figure C.0.7. Vigenère's Tableau
Updated Vigenère Tableau
svgpngpdf
Figure C.0.8. Updated Vigenère Tableau
This is a copy of Vigenère's Auotkey Table.
svgpngpdf
Figure C.0.9. Vigenère's Autokey Tableau
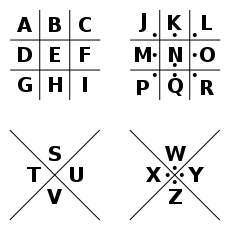
Cipher Key for the Pigpen Cipher
svgpngpdf
Figure C.0.10. Pigpen Cipher Key
Table C.0.11. Falconer's Transposition Table
A B C
1 \(\phantom{WWWWW}\) \(\phantom{WWWWW}\) \(\phantom{WWWWW}\) \(\phantom{WWWWW}\)
2 \(\phantom{WWWWW}\) \(\phantom{WWWWW}\) \(\phantom{WWWWW}\)
3 \(\phantom{WWWWW}\) \(\phantom{WWWWW}\) \(\phantom{WWWWW}\)
4 \(\phantom{WWWWW}\) \(\phantom{WWWWW}\) \(\phantom{WWWWW}\)
5 \(\phantom{WWWWW}\) \(\phantom{WWWWW}\) \(\phantom{WWWWW}\)
6 \(\phantom{WWWWW}\) \(\phantom{WWWWW}\) \(\phantom{WWWWW}\)
Kasiski Key Table
svgpngpdf
Figure C.0.12. Kasiski Key Table
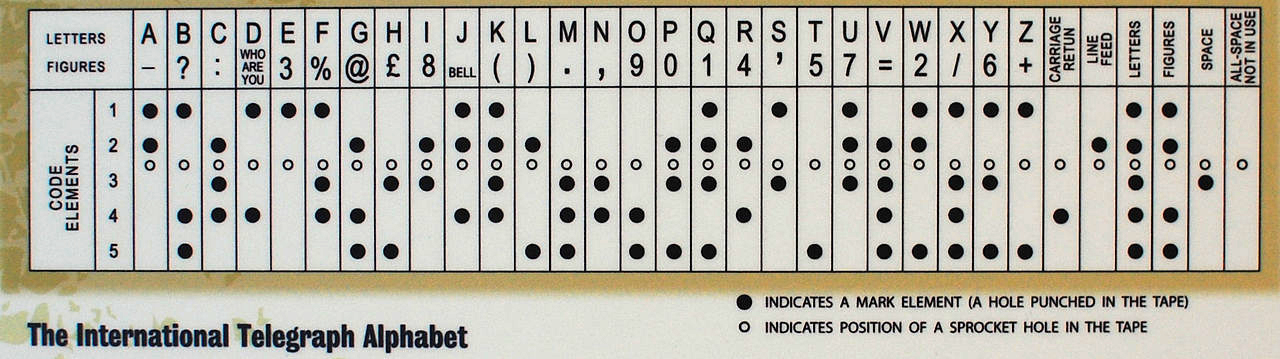
International Telegraph Alphabet 2 ca. 1924
svgpng
Figure C.0.13. International Telegraph Alphabet 2 ca. 1924
Multiplication table modulo 26
svgpngpdf
Figure C.0.14. Multiplication table modulo 26
Table C.0.15. ASCII Code Chart
\(b_7\, b_6\, b_5 \rightarrow \) 000 001 010 011 100 101 110 111
\(\downarrow b_4\, b_3\, b_2\, b_1\) 0 16 32 48 64 80 96 112
0000 0 NUL DLE ␣ 0 @ P ` p
0001 1 SOH DC1 ! 1 A Q a q
0010 2 STX DC2 " 2 B R b r
0011 3 ETX DC3 # 3 C S c s
0100 4 EOT DC4 $ 4 D T d t
0101 5 ENQ NAK % 5 E U e u
0110 6 ACK SYN & 6 F V f v
0111 7 BEL ETB ' 7 G W g w
1000 8 BS CAN ( 8 H X h x
1001 9 TAB EOM ) 9 I Y i y
1010 10 LF SUB * : J Z j z
1011 11 VT ESC + ; K [ k \(\{\)
1100 12 FF FS , < L \(\backslash\) l |
1101 13 CR GS - = M ] m \(\}\)
1110 14 SO RS . > N \(\wedge\) n \(\sim\)
1111 15 SI US / ? O \(\_\) o DEL
This figure gives an outline of the workings of a feistel style cipher.
svgpngpdf
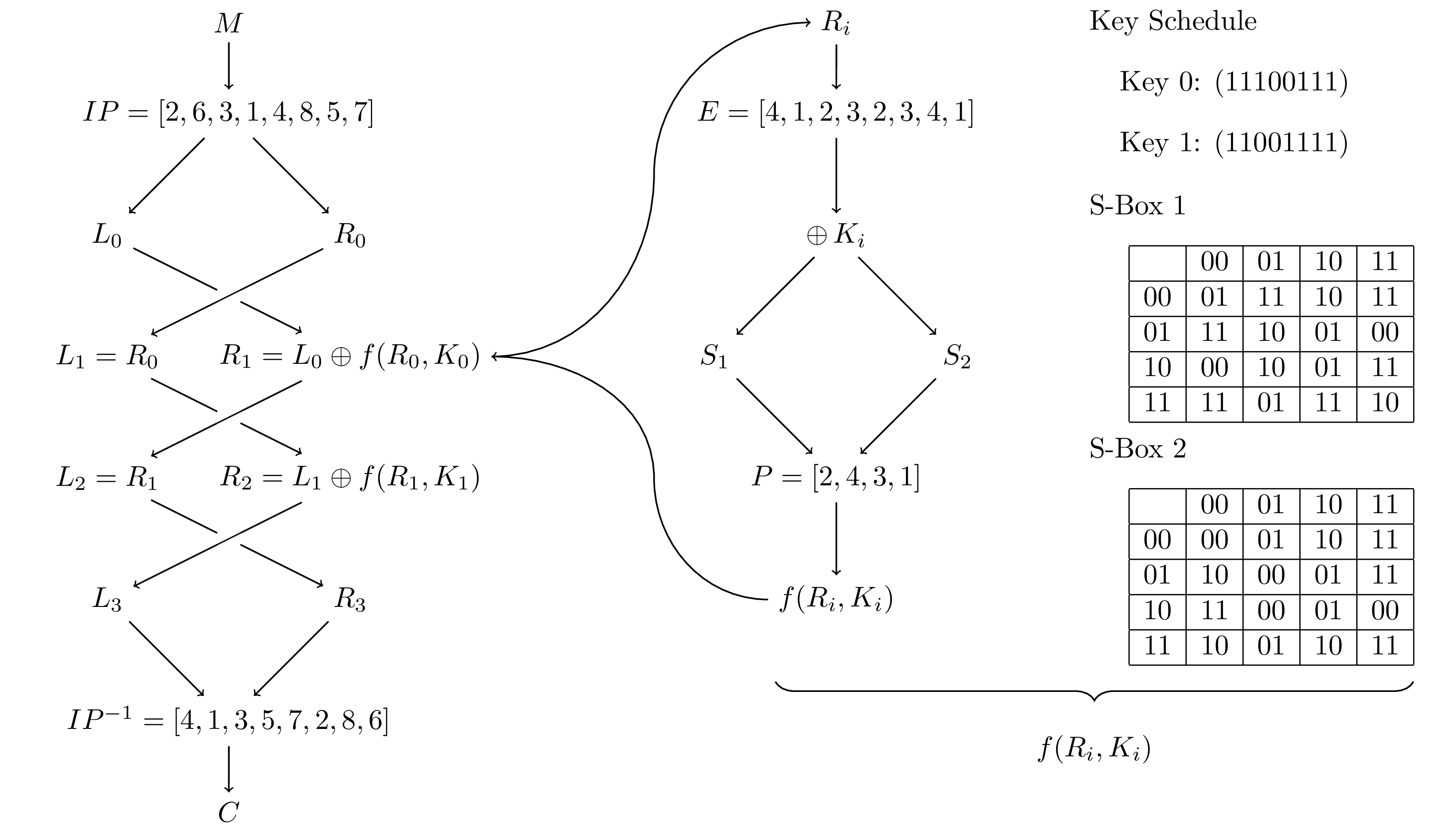
Figure C.0.16. Outline of a Feistel Cipher
This is a highly simplified example of the Data Encryption Standard
svgpngpdf
Figure C.0.17. A Highly Simplified two step DES
svgpngpdf
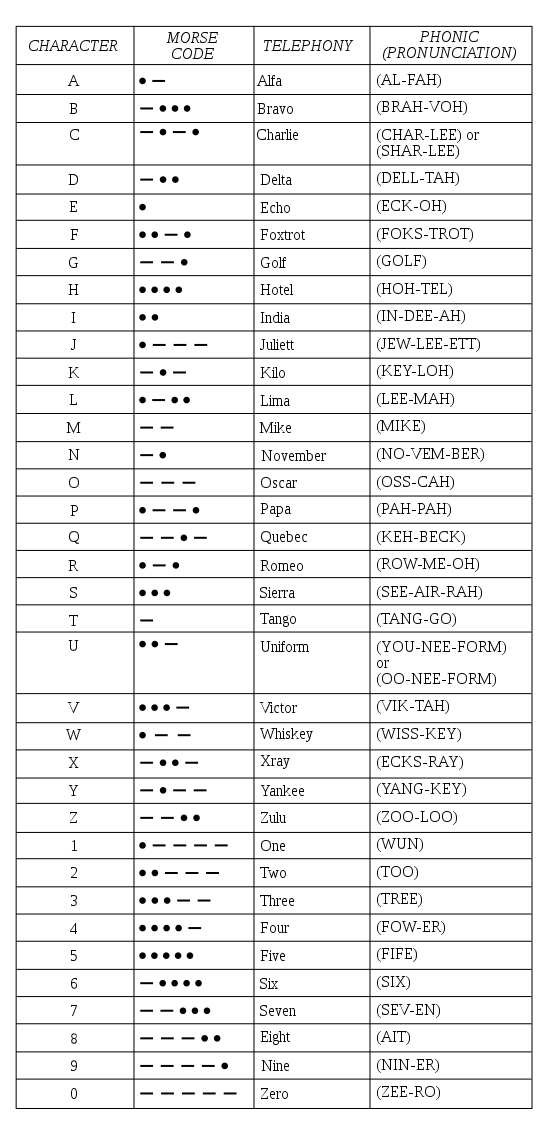
Figure C.0.18. NATO Phonetic Alphabet (from Wikimedia Commons)