Skip to main content

Section 7.2 Data Encryption Standard

Subsection 7.2.1 A Little History

Subsection 7.2.2 Overview Really Simple DES

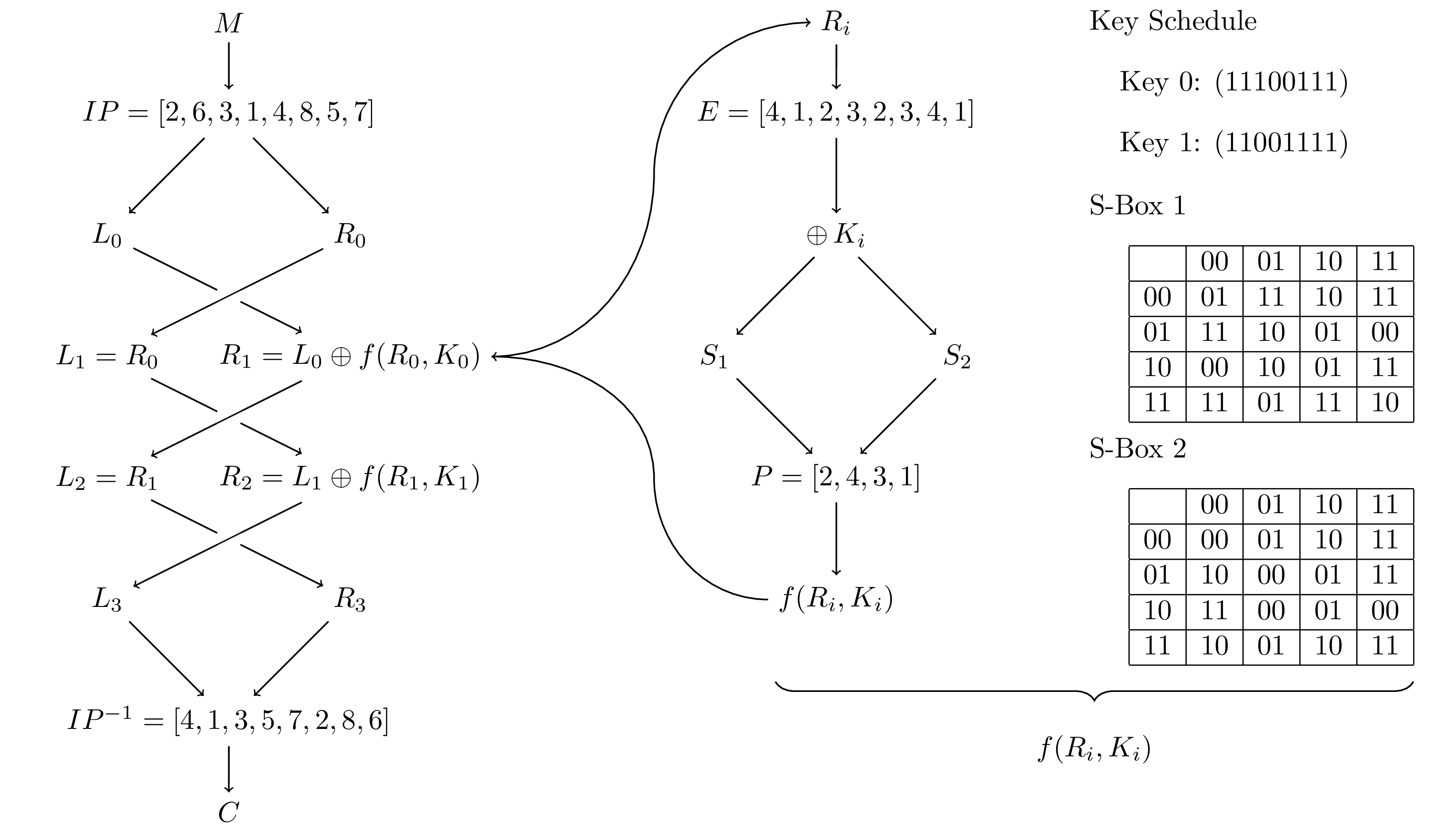
The algorithm for the really simple data encryption standard follows this general pattern:

  1. Create a Key Schedule, assume the keys are each 8 bits; a group of 8 bits is called a byte
  2. Convert the input into a stream of bits
  3. Split the bit stream into bytes
  4. Permute the entries in each byte
  5. Run the permuted byte through two enciphering rounds with the function\(f(R_i,K_i)\)
  6. Swap the left and right in the final round
  7. Apply the inverse of the initial permutation

The diagram below gives a little more detail and we will walk through this a bit at a time in this section.

This is a highly simplified example of the Data Encryption Standard
svgpngpdf
Figure 7.2.1. A Highly Simplified two step DES

Starting with the initial 32 bit key:

\begin{equation*} K=11100111 10010101 00010011 10001001 \end{equation*}

we generate a key schedule in which key 0 consists of bits 1 through 8, key 1 is bits 2 through 9, key 3 is bits 3 through 10, etc.. Doing this the first five keys are:

\begin{gather*} Key\ 0=11100111\\ Key\ 1=11001111\\ Key\ 2=10011110\\ Key\ 3=00111100\\ Key\ 4=01111001\\ Key\ 5=11110010 \end{gather*}

Continuing with the main key:

\begin{equation*} K=11100111 10010101 00010011 10001001 \end{equation*}

find keys \(Key\ 6\text{,}\) \(Key\ 7\text{,}\) and \(Key\ 8\text{.}\)

Answer
\begin{gather*} Key\ 6=11100101\\ Key\ 7=11001010\\ Key\ 8=10010101 \end{gather*}

Using the key:

\begin{equation*} K_2=11100100 10001000 10001111 00010010 \end{equation*}

find keys \(Key\ 0\text{,}\) \(Key\ 1\text{,}\) \(Key\ 2\text{,}\) and \(Key\ 3\text{.}\)

Answer
\begin{gather*} Key\ 0=11100100\\ Key\ 1=11001001\\ Key\ 2=10010010\\ Key\ 3=00100100 \end{gather*}

Suppose we want to encipher “bye” using the Table 7.1.14 we get:

\begin{equation*} bye\equiv(1100010 1111001 1100101) \end{equation*}

which we expand to

\begin{equation*} bye\equiv(00011000 10111100 11100101) \end{equation*}

the the number of bits is a multiple of 8. Now spliting this into bytes we get three pieces:

\begin{gather*} M_1=(00011000)\\ M_2=(10111100)\\ M_3=(11100101) \end{gather*}

Next we will need to look at how we permute the bits in each sub piece in order to start enciphering.

Suppose we want to encipher “hi”. Use Table 7.1.14 to convert this to bits, and then split it up into bytes.

Hint

Be sure to look back at Subsection 7.1.2 to review looking up characters in the ASCII table. Also, remember to tack on a couple of extra 0 bits at the start in order to make the length of the message a multiple of 8.

Answer
\begin{gather*} M_1=(00110100)\\ M_2=(01101001) \end{gather*}

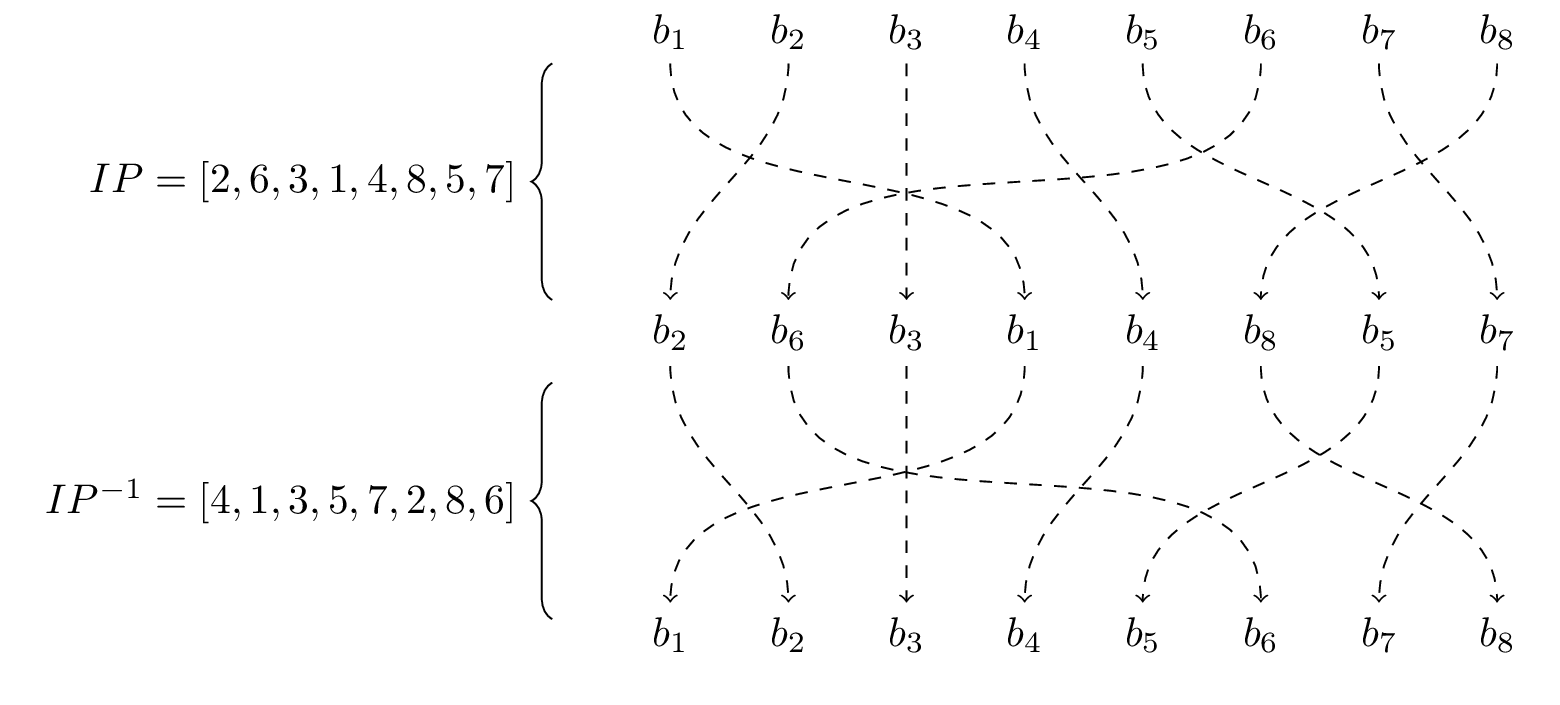
Subsection 7.2.3 Permutation

As part of the encryption process each byte of information will be run through a fixed initial permutation before enciphering and through the inverse of the permutation at the end. The permutation we will be using is:

\begin{equation*} IP=[2,6,3,1,4,8,5,7]. \end{equation*}

We read this as:

  • move bit 1 to position 4
  • move bit 2 to position 1
  • move bit 3 to position 3
  • move bit 4 to position 5
  • move bit 5 to position 7
  • move bit 6 to position 2
  • move bit 7 to position 7
  • move bit 8 to position 6
diagram of the permutations used at the very start and end of the permutation process
svgpngpdf
Figure 7.2.7. Initial and Terminal Permutations for DES

Once we have completed all the rounds of the Feistel cipher that is at the heart of DES we will apply the inverse permutation:

\begin{equation*} IP^{-1}=[4,1,3,5,7,2,8,6]. \end{equation*}

As we can see in Figure 7.2.7 if there were no intermediate steps this would just give us back the exact same byte.

If we take the first byte in our example above

\begin{equation*} M_1=(0 0 0 1 1 0 0 0) \end{equation*}

and permute it we get

\begin{equation*} IP\left(M_1\right)=(0 0 0 0 1 0 1 0). \end{equation*}

We can then split this into left and right nibbles (a set of 4 bits, and in case you were wondering 2 bits is a crumb) in preparation for enciphering:

\begin{gather*} L_0=(0 0 0 0)\\ R_0=(1 0 1 0). \end{gather*}

If you started with \(M_1=(00110100)\) what would you get by applying \(IP\) and then splitting the message into \(L_0\) and \(R_0\text{?}\)

Answer

\(L_0=0110\) and \(R_0=1000\)

Subsection 7.2.4 Enciphering Function

Now that we have an initial pair of left and right nibbles we are ready to start the process of shuffling them together with our Feistel cipher. As usual

\begin{equation*} L_1=R_0 \end{equation*}

and

\begin{equation*} R_1=L_0\oplus f(R_0,K_0)\text{.} \end{equation*}

But unlike the simple \(f\) in Section 7.1, here the function combining \(R_0\) and \(K_0\) is devilishly complicated; this is what gives DES its strength.

  1. Expand the right half to 8 bits
  2. Add the round key
  3. Use the S-boxes to reduce the 8-bits back to 4
  4. Permute the 4 bits

The first couple of steps and the last step are fairly straight forward and we will look at them just below. They work in ways similar to the permutation above and to the Feistel cipher we had discussed before. The third step will need more discussion.

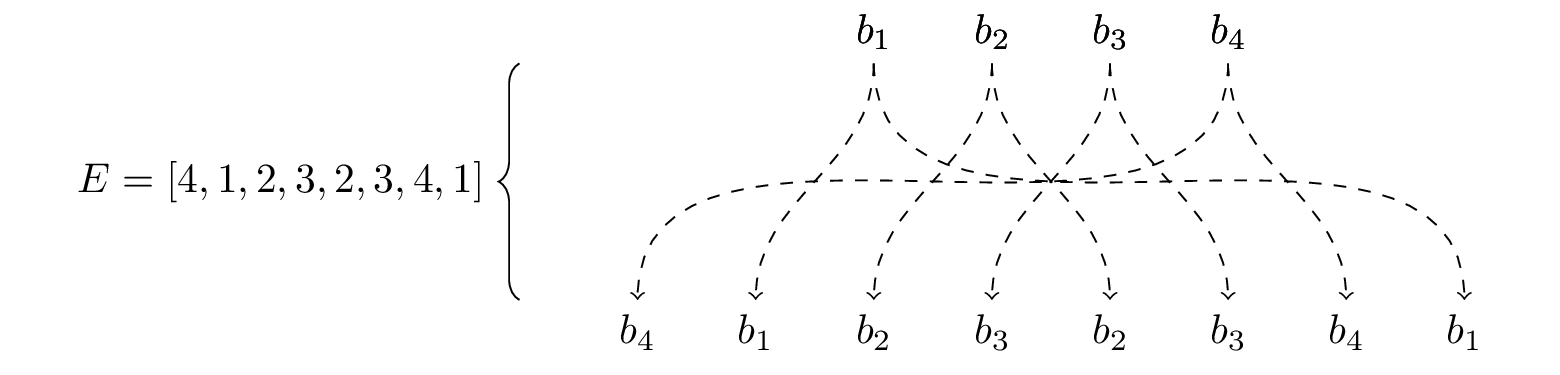
The first step in the round function is to expand the 4-bit nibble \(R_i\) into an 8-bit byte so that it can be added to the round key \(K_i\text{.}\) This is expressed in the diagram as

\begin{equation*} E=[4,1,2,3,2,3,4,1] \end{equation*}

which we read in much the same way we read the initial permutation \(IP\text{.}\)

We read \(E\) as:

  • copy bit 1 to positions 2 and 8
  • copy bit 2 to positions 3 and 5
  • copy bit 3 to positions 4 and 6
  • copy bit 4 to positions 1 and 7
diagram of the expansion used in each round of the enciphering process
svgpngpdf
Figure 7.2.10. Expansion in the round function for DES

Once this is done we can add the expanded right side and the key as we have before:

\begin{align*} E(R_i)\oplus K_i\amp =(b_4,b_1,b_2,b_3,b_2,b_3,b_4,b_1)\oplus (k_1,k_2,k_3,k_4,k_5,k_6,k_7,k_8)\\ \amp = (b_4\oplus k_1,b_1\oplus k_2,b_2\oplus k_3,b_3\oplus k_4,b_2\oplus k_5,b_3\oplus k_6,b_4\oplus k_7,b_1\oplus k_8) \end{align*}

The initial left and right nibbles are

\begin{equation*} L_0=(0 0 0 0)\ \text{and}\ R_0=(1 0 1 0). \end{equation*}

The next left side is \(L_1=R_0=(1 0 1 0)\text{.}\) To find the next right side we first run \(R_0\) and \(K_0\) through the round function which begins by expanding and adding the key.

\begin{align*} E(1010)\oplus K_0\amp = (0 1 0 1 0 1 0 1)\oplus (1 1 1 0 0 1 1 1)\\ \amp = (1 0 1 1 0 0 1 0). \end{align*}

The result of this needs to be run through the s-boxes to compress this output back to a nibble.

What do we get if we expand \(R_0=1000\) and add it to the key \(k_0=11100100\)

Answer
\begin{align*} E(R_0)\amp=01000001\\ E(R_0)\oplus k_0\amp=10100101 \end{align*}

The s-boxes serve the opposite roll of the expansion; they turn bytes into nibbles. To compress the byte,

  1. split it into two nibbles,
  2. run the first nibble through s-box 1,
  3. run the second nibble through s-box 2, and
  4. put the output crumbs back together into a single nibble.

We send a nibble through an s-box by using the first two bits as the row label and the second as a column label, where they intersect is the output. For example in s-box 1 below the nibble (1101) leads us to row (11) and column (01) so that the output is (01).

Table 7.2.13. S-Box 1
00 01 10 11
00 01 11 10 11
01 11 10 01 00
10 00 10 01 11
11 11 01 11 10
Table 7.2.14. S-Box 2
00 01 10 11
00 00 01 10 11
01 10 00 01 11
10 11 00 01 00
11 10 01 10 11

After expanding and adding the key we are left with the byte \((10 11 00 10)\) which gives two nibbles:

\begin{equation*} n_1=(10 11)\ \text{and}\ n_2=(00 10). \end{equation*}

Running \(n_1\) through s-box 1 we get (11) and \(n_2\) through s-box 2 gives (10). These combine to give the nibble (1110).

The last step is to apply the permutation \(P=[2,4,3,1]\) to get:

\begin{equation*} f\left(R_0,K_0)=(1011)\right). \end{equation*}

Adding this to \(L_0=(0000)\) we finally get

\begin{align*} R_1\amp = L_0\oplus f\left(R_0,K_0\right)\\ \amp = (0000)\oplus(1011)\\ \amp = (1011). \end{align*}

Use the s-boxes to compress \((10100101)\) down to a nibble and apply the final permutation \(P\text{.}\)

Answer

\(f(R_0,k_0)=1000\)

Subsection 7.2.5 Finishing Enciphering

Looking at Figure 7.2.1 we see that we run the left and right pieces through the cipher function two times total, swap the sides so that deciphering will work identically to enciphering, and finally apply the inverse of the initial permutation.

Starting with \(M_1=(0 0 0 1 1 0 0 0)\) we now have:

\begin{equation*} L_1=(1 0 1 0)\ \text{and}\ R_1=(1 0 1 1). \end{equation*}

Running through second full round gives us \(L_2=(1011)\) and

\begin{align*} R_2\amp = L_1\oplus f(R_1,K_1)\\ \amp = (1010)\oplus (1111)\\ \amp = (0101) \end{align*}

Swapping sides without using the function gives

\begin{equation*} L_3=(0 1 0 1)\ \text{and}\ R_3=(1 0 1 1). \end{equation*}

Finally putting these together, (0101 1011), and applying \(IP^{-1}\) we get

\begin{equation*} C_1=(10011110). \end{equation*}

Given \(L_1=1000\) and \(R_1=1110\) use the key \(k_1=11001001\) to go through another round with the enciphering function, and then finish the enciphering process.

Answer
\begin{align*} L_2\amp =1110\ \text{and}\ R_2=0011\\ L_3\amp =0011\ \text{and}\ R_3=1110\\ C\amp =10111001 \end{align*}

Subsection 7.2.6 A Little More Practice

(a)

Apply the initial permutation IP to \(M_2=(10111100)\) and split it into \(L_0\) and \(R_0\text{.}\)

Answer

\(L_0=0111\) and \(R_0=1010\)

(b)

Expand \(R_0\) with \(E=[4,1,2,3,2,3,4,1]\) and add round key \(Key\ 2=10011110\text{.}\)

Answer

\(E(R_0)\oplus K_2 = 1100\, 1011\)

(c)

Apply the s-boxes to \(E(R_0)\oplus K_2 = 1100\, 1011\) to reduce it to a nibble, and then apply the permutation \(P=[2,4,3,1]\text{.}\)

Answer

\(f\left(R_0,K_2\right)=1001\)

(d)

Add \(f\left(R_0,K_2\right)=1001\) to \(L_0\) in order to get \(R_1\text{.}\)

Answer

\(L_1=1010\) and \(R_1=1110\)

(e)

Run \(L_1=1010\) and \(R_1=1110\) through another full round using the \(Key\ 3=00111100\) in order to get \(L_2\) and \(R_2\text{.}\)

Answer

\(L_2=1110\) and \(R_2=0111\)

(f)

Swap the left and right sides one more time, without applying the function, and then apply \(IP^{-1}\) to get \(C_2\text{.}\)

Answer

\(C_2=10111101\)

(a)

Apply the initial permutation IP to \(M_3=(11100101)\) and split it into \(L_0\) and \(R_0\text{.}\)

Answer

\(L_0=1111\) and \(R_0=0100\)

(b)

Expand \(R_0\) with \(E=[4,1,2,3,2,3,4,1]\) and add round key \(Key\ 4=01111001\text{.}\)

Answer

\(E(R_0)\oplus K_4 = 0101\, 0001\)

(c)

Apply the s-boxes to \(E(R_0)\oplus K_4 = 1100\, 1011\) to reduce it to a nibble, and then apply the permutation \(P=[2,4,3,1]\text{.}\)

Answer

\(f\left(R_0,K_4\right)=0101\)

(d)

Add \(f\left(R_0,K_4\right)=0101\) to \(L_0\) in order to get \(R_1\text{.}\)

Answer

\(L_1=0100\) and \(R_1=1010\)

(e)

Run \(L_1=0100\) and \(R_1=1010\) through another full round using the \(Key\ 5=11110010\) in order to get \(L_2\) and \(R_2\text{.}\)

Answer

\(L_2=1010\) and \(R_2=1010\)

(f)

Swap the left and right sides one more time, without applying the function, and then apply \(IP^{-1}\) to get \(C_3\text{.}\)

Answer

\(C_3=01111000\)

Suppose that there is a fourth part to our message \(M_4=01110011\text{.}\)

(a)

Apply \(IP\) to \(M_4\) and split it to get \(L_0\) and \(R_0\text{.}\)

Answer

\(L_0=1010\) and \(R_0=1101\)

(b)

Now find the next set of nibbles \(L_1\) and \(R_1\text{,}\) use the round key \(Key\ 6=11100101\text{.}\)

Answer

\(L_1=1101\) and \(R_1=0000\)

(c)

Now find the next set of nibbles \(L_2\) and \(R_2\text{,}\) use the round key \(Key\ 7=11001010\text{.}\)

Answer

\(L_2=0000\) and \(R_2=0000\)

(d)

Now find the next set of nibbles \(L_3\) and \(R_3\text{.}\)

Answer

\(L_3=0000\) and \(R_3=0000\)

(e)

Finish up the enciphering process.

Answer

\(C_4=0000 0000\)

Decipher the message \(C=10000100\) which was enciphered using the two keys \(k_2=10010010\) and \(k_3=00100100\text{.}\)

Hint
  1. Recall that the enciphering and deciphering algorithms are identical.
  2. Remember to reverse the order in which you use the keys when deciphering the message.
Answer

\(M=01101001\)

Comments on Full DES.