Skip to main content

Section 5.2 Perfect Secrecy

Subsection 5.2.1 Telegraphs and Teletype

By the middle of the nineteenth century the invention of the telegraph by Samuel Morse had made high speed communication a reality. The telegraph allowed people to send signals, short bursts of electricity, along wires from one point to another. The signals were initiated with a key and received with a sounder (figure Figure 5.2.2). But, the sounder didn't generate any sort of sophisticated sound like the telephone would, it just generated beeps or buzzes. What was needed was a code.

The answer to this came from Samuel Morse. Morse code would translate letters into a series of dots, \(\cdot\), and dashes, \(-\), which the telegraph sounder indicated with shorter beeps and longer beeps (see table Table 5.2.1).

Table 5.2.1. Morse Code
A: \(.-\) B: \(-...\) C: \(-.-.\) D: \(-..\) E: \(.\) F: \(..-.\) G: \(--.\) H: \(....\)
I: \(..\) J: \(.---\) K: \(-.-\) L: \(.-..\) M: \(--\) N: \(-.\) O: \(---\) P: \(.--.\)
Q: \(--.-\) R: \(.-.\) S: \(...\) T: \(-\) U: \(..-\) V: \(...-\) W: \(.--\) X: \(-..-\)
Y: \(-.--\) Z: \(--..\)
Image of a telegraph key and sounder
Figure 5.2.2. Telegraph Key and Sounder

While a skilled telegraph operator could send dozens of words per minute they were no match for the industrial revolution and machines. The Jacquard Loom developed around 1804 used a series of cards with holes punched into them to mechanize the process of weaving. It was soon realized that information other than fabric patterns could be encoded in this way. Charles Babbage and Ada Lovelace used this idea to try and create a programmable mechanical computer over one hundred years prior to the invention of the electronic computer in the 1940's. In the latter half of the nineteenth century it was also realized that messages could be encoded on card or paper tape in this same way and then read at high speed by a machine. These machines eventually evolved into tape readers such as the Creed Model Tape Reader in figure Figure 5.2.3. But to do this there was a need for a new code.

Image of a 1924 Creed Model Tape Reader
Figure 5.2.3. Creed Model Tape Reader ca. 1924
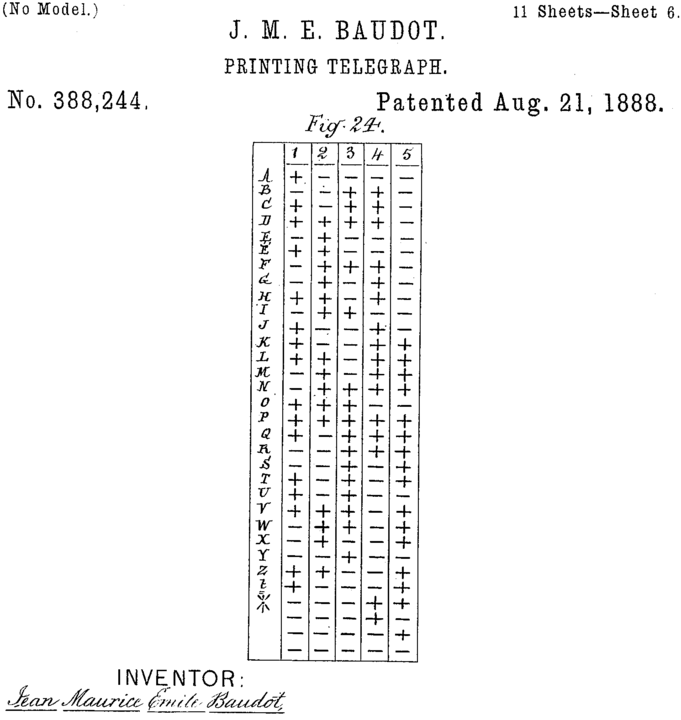
Baudot's Printing Telegraph Code from 1888
Figure 5.2.4. Baudot's Printing Telegraph Code from 1888

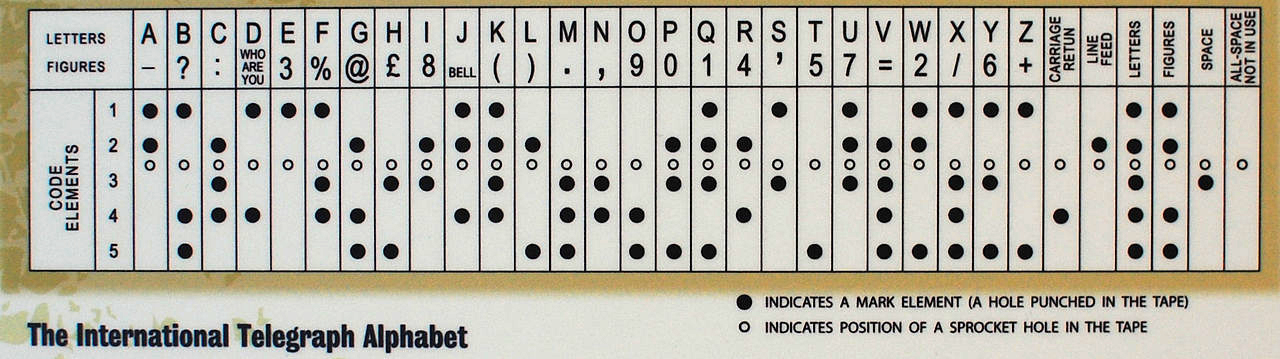
One early candidate came from Émile Baudot in 1888 (see figure Figure 5.2.4). In his patent he represented characters abstractly using pluses and minuses, where a plus would represent a hole in a punch card and a minus would represent not a hole. Donald Murray modified this around 1901 and his code eventually evolved into the International Telegraph Alphabet like the one in figure Figure 5.2.5.

International Telegraph Alphabet 2 ca. 1924
Figure 5.2.5. International Telegraph Alphabet 2 ca. 1924

Comprehension Check:

  • Looking at figures Figure 5.2.5, how many dots are used to represent “E”?
  • Looking at figures Figure 5.2.5, how many dots are used to represent “T”?
  • Looking at figures Figure 5.2.5, how many dots are used to represent “V”?
  • How do your previous answers compare to how these letters are represented the Morse code in table Table 5.2.1?
  • If you compare this to what you know about letter frequencies, can you make a conjecture about the number or dots used to represent a letter and the letter's frequency?
  • From the practical standpoint of using/implementing these codes, why do you think the creators made this choice?

Subsection 5.2.2 Gilbert S. Vernam and His Great Plan

All the codes discussed above were not codes or ciphers as we have discussed them previously. These codes did not serve to obfuscate meaning, their roll was to facilitate high speed communications. So, in this age of the machine how can we keep a message secure? One way to do this would be to encipher a message by hand, transmit the enciphered message mechanically, and finally decipher that message by hand. This, however, would be a suboptimal solution to this problem in an industrial age.

In 1919, just five years after completing college at Worcester Polytechnic Institute, Gilbert S. Vernam had an idea. He proposed a system in which you would feed two paper tapes through a machine at the same time. On one tape would be the message that you wanted to send and on the other would be a random string of characters which acted as a key. The machine would translate both strings of characters into teletype code and then “add” them together using an exclusive or operation (in modern computers this is now called bitwise addition). The recipient of the message would using an identical copy of the key and identical machine could then decipher it.

Gilbert S. Vernam Secret Signaling System Patent
Figure 5.2.6. Gilbert S. Vernam Secret Signaling System Patent

Subsubsection 5.2.2.1 Comments on Circuits and Logic

Before looking at an excerpt from Vernam's 1919 patent we need to learn a little about the idea of an exclusive or and how we can visualize it using an electrical circuit.

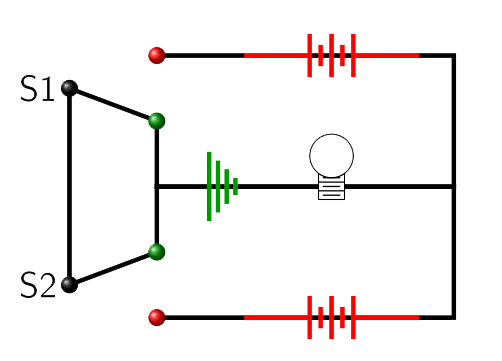
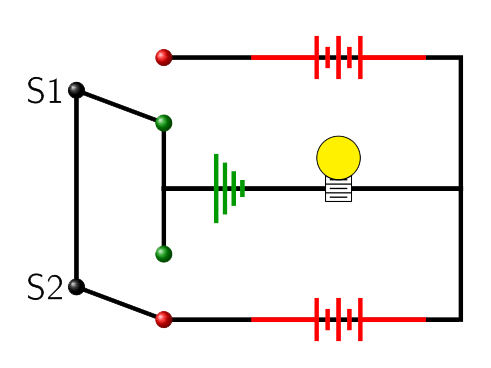
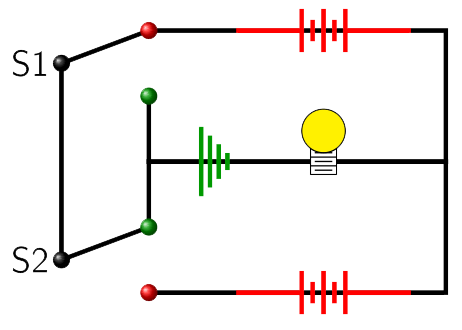
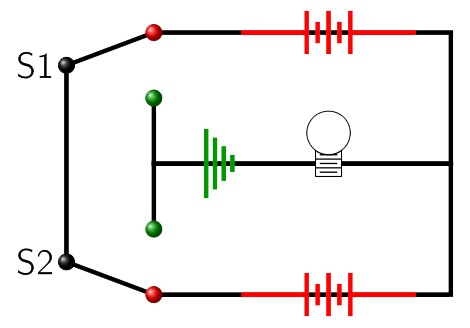
In order to complete a circuit and light a light bulb, the bulb needs to be connected to both sides of a battery and the circuit must pass through a ground connection (Figure 5.2.7). For this discussion, we will say a switch is on if it is switched toward the battery and off if it is switched toward ground. With all of this in mind take a careful look at figures Figure 5.2.8 through Figure 5.2.11 and then try to answer the comprehension questions below them.

Symbols for Batteries and Ground
svgpng
Figure 5.2.7. Battery and Ground
Open circuit with both contacts to ground
svgpng
Figure 5.2.8. Open circuit with both contacts to ground
Closed circuit with one contact to ground and one to a battery
svgpng
Figure 5.2.9. Closed circuit with one contact to ground and one to a battery
Closed circuit with one contact to a battery and one to ground
svgpng
Figure 5.2.10. Closed circuit with one contact to a battery and one to ground
Open circuit with both contacts to batteries
svgpng
Figure 5.2.11. Open circuit with both contacts to batteries

Comprehension Check:

  • Looking at figure Figure 5.2.8, why isn't the bulb lit up? What positions are the switches S1 and S2 in?
  • Looking at figure Figure 5.2.11, why isn't the bulb lit up? What positions are the switches S1 and S2 in?
  • Looking at figures Figure 5.2.9 and Figure 5.2.10, why are the bulbs lit up? What positions are the switches S1 and S2 in?
  • In the circuit shown in the figures, which combinations of switch positions light up the bulb and which do not?

  • Assuming \(+\) means on and \(-\) means off which of the following combinations light up the bulb

    • S1=\(-\) and S2=\(-\)
    • S1=\(-\) and S2=\(+\)
    • S1=\(+\) and S2=\(-\)
    • S1=\(+\) and S2=\(+\)

This sort of circuit is referred to as an exclusive or, XOR, circuit in reference to the term XOR from mathematical logic.

Definition 5.2.12. Logical Exclusive Or.

If we combine two statements \(P\) and \(Q\) with an exclusive or then the compound statement, \(P\ XOR\ Q\text{,}\) is true when precisely one of the statements is true. This is sometimes represented in a truth table like so

Table 5.2.13. Exclusive Or Truth Table
\(P\) \(Q\) \(P\bigoplus Q\)
False False False
False True True
True False True
True True False

Notationally the XOR is written with the symbol \(\bigoplus\text{.}\) In some settings “False” may be represented by a “0” or “\(-\)” sign and True may be represented by a “1” or “\(+\)” sign.

Subsubsection 5.2.2.2 Vernam's Plan

What follows is Vernam's description of how his Secret Signaling System enciphers a character. The numbers in the paragraph correspond to labels in the circuit diagram in his 1919 patent. For us the numbers are important as a way of referring to steps in the process, try not to let them overwhelm you. But remember it is okay to be confused and struggle, that is how we learn.

Let us suppose that the first character of the message to he transmitted is “A.” The code signal of “A” is “\(++---\text{,}\)” where “\(-\)” represents an “open” or “spacing” impulse and “\(+\)” represents a “closed” or “marking” impulse in the system here illustrated, although it will be understood that positive and negative current impulses may be used instead of closed and open circuit operation if desired. For ciphering and deciphering the message the ciphering devices at the opposite ends of the line are provided with identical sections of tape upon which are recorded a series of code signals which are preferably selected at random but if desired may themselves represent a predetermined series of letters or words. Let us suppose that the letter “B” happens to be in the ciphering transmitter at the same moment that the letter “A” is being sent from the normal transmitter. The code for the letter “B” is “\(+--++\text{.}\)” The sending of “A” from the normal transmitter means that the contacts 25 and 26 will be closed, while the contacts 27, 28 and 29 are open. Thus, relays 14 and 15 will be energized and close their contacts, while relays 16, 17 and 18 remain unenergized. The presence of the letter “B” in the code transmitter means that contacts 36, 39 and 40, representing the plus impulses for “B,” will be in contact with the bus-bar 32, which is connected to [the] battery and that contacts 37 and 38, representing the negative impulses for this character will be in contact with bus-bar 33 which is grounded.

As a result of this combination of contacts in the two transmitters, it will be seen that the relay 19 is connected at both ends to a battery; that relay 20 is connected at one end to a battery at 24 and at the other end to ground at 35; that relay 21 is connected at one end to ground through the resistance 31, and at the other end to ground at 35 ; that relay 22 is connected at one end to ground through resistance 31, and at the other end to battery at 34, and that relay 23 is connected to ground through the resistance 31 at one end and the battery 34 at the other. Therefore, relays 20, 22 and 23 will close their contacts; and relays 19 and 21 will remain open. Consequently, as the distributer arm 10 rotates over the contacts 1 to 5, impulses will be transmitted to the line from contacts 2, 4 and 5 and none from contacts 1 and 3. This means that the signal “\(-+-++\)” will be transmitted over the line and this signal represents the letter “G” and not the letter “A” which is the character of the message to be transmitted.

Comprehension Check:

  • Which combination of \(+\)'s and \(-\)'s represent the letter A?
  • Which combination of \(+\)'s and \(-\)'s represent the letter B?
  • The letter G is represented by (\(-+-++\)). Look at the representations of A and B and the definition of exclusive or (Definition 5.2.12), use these to explain how we arrived at the representation of G.
  • Vernam says that the “relay 19 is connected at both ends to a battery” and so will remain open. Comparing this to the questions you answered about figures Figure 5.2.8 through Figure 5.2.11 what do you notice?
  • Vernam says that the “relay 20 is connected at one end to a battery at 24 and at the other end to ground at 35” and so it will close. Comparing this to the questions you answered about figures Figure 5.2.8 through Figure 5.2.11 what do you notice?
  • Repeat the previous two questions for relays numbered 21, 22, and 23.

Using the ITA2 codes (figure Figure 5.2.5) we can write E as (\(+----\)) and write Q as (\(+++-+\)). Add these together using the exclusive or operation just like Vernam added A and B.

Hint

You can use the truth table Table 5.2.13 to help you if you recall that \(+\) is True and \(-\) is False.

Answer

You should get (\(-++-+\)) which is P.

Using the ITA2 codes (figure Figure 5.2.5) we can write U as (\(+++--\)) and write H as (\(--+-+\)). Add these together using the exclusive or operation just like Vernam added A and B.

Hint

You can use the truth table Table 5.2.13 to help you if you recall that \(+\) is True and \(-\) is False.

Answer

You should get (\(++--+\)) which is W.

Using the ITA2 codes (figure Figure 5.2.5) look up the codes for F and T. Add these together using the exclusive or operation just like Vernam added A and B.

Hint

When you read the ITA2 table you should read top to bottom with \(+\equiv\bullet\) and \(-\equiv \circ\)(a blank space)

Answer

You should get (\(+-+++\)) which is X.

Using the ITA2 codes (figure Figure 5.2.5) look up the code for K. Add K to its self using the exclusive or operation just like Vernam added A and B.

Hint

When you read the ITA2 table you should read top to bottom with \(+\equiv\bullet\) and \(-\equiv \circ\)(a blank space)

Answer

You should get (\(-----\)) which is listed as not in use.

After the above passage Vernam, with some more reference to the circuit diagram for his device, goes on to explain how deciphering is identical to enciphering. For example to encipher we added A (\(++---\)) to B (\(+--++\)) to get G (\(-+-++\)). To decipher the person receiving the message will add B to G and recover A.

Comprehension Check:

  • Add B (\(+--++\)) to G (\(-+-++\)), does this in fact return A (\(++---\))?
  • Verify that adding C (\(-+++-\)) and D (\(+--+-\)) gives U (\(+++--\)). Then add D to U, do you get C back?
  • What happens when you add B to B?
  • What happens when you add M to M?
  • What happens when you add F to F?
  • What will happen if you add any letter to its self?
  • Can you explain in terms of exclusive or (definition Definition 5.2.12) why you got the results you did for the previous few questions?

Encipher the word “hello” by adding the key “ABCHE”

Hint

Translate the letters into code using figure Figure 5.2.5. Then, add the letters one character at a time, i.e. start with \(H\bigoplus A\) then proceed from there.

Answer

You should get the ciphertext “QOMIB”.

Encipher the word “pizza” by adding the key “ATTACK”

Hint

Translate the letters into code using figure Figure 5.2.5. Then, add the letters one character at a time, i.e. start with \(P\bigoplus A\) then proceed from there.

Answer

You should get the ciphertext “YPELFR”.

Decipher the text “GYTVS” by adding the key “QWYRT”.

Hint

Translate the letters into code using figure Figure 5.2.5. Then, add the letters one character at a time, i.e. start with \(G\bigoplus Q\) then proceed from there.

Answer

You should get the plaintext “fishy”.

Decipher the text “GOANBZT” by adding the key “BHFOEKS”

Hint

Translate the letters into code using figure Figure 5.2.5. Then, add the letters one character at a time, i.e. start with \(G\bigoplus B\) then proceed from there.

Answer

You should get the plaintext “anchovy”.

Subsection 5.2.3 Vigenère and Perfect Secrecy

Subsubsection 5.2.3.1 Vigenère Perfected

There are two ways in which we can compare Vigenère's cipher to Vernam's plan. First, we can encipher a length of plain text, “Bright vixens jump; dozy fowl quack,” using Vigenère's cipher and a random key that is equal in length to the plain text like so

Table 5.2.22. Vigenère Perfected
KEY: HEPYT DMAWP TWQMF TALTE MTFDQ PTNS
plain: brigh tvixe nsjum pdozy fowlq uack
CIPHER: IVXEA WHITT GOZGR IDZSC RHBOG JTPC

Then, the plaintext is one of the input tapes in Vernam's system, the key is the other input tape, and the ciphertext is the output. The other way to compare the two systems is to recognize that each row in the modern Vigenère table (figure Figure C.0.8) is a shift, row “A” is shifted by 0, row “B” by 1, row “C” by 2, etc. Thus when we encipher a “b” with the key letter “H” to get the cipher “I” we can picture it as addition \(1+7=8\text{.}\)

Subsubsection 5.2.3.2 Perfect Secrecy

Write so stuff...

What Vernam's system offers is a system which if used correctly offers absolute unbreakable security, this is called perfect secrecy. To understand what this means from a technical standpoint we need a couple definitions.

Definition 5.2.23. Plaintext, Ciphertext, and Key Spaces.

The plaintext, ciphertext, and key spaces are the sets of all possible plaintexts, ciphertexts, and keys for an encryption system.

The plaintext space is all the messages you may wish to send and the ciphertext space is all the ways those message may be enciphered, while important they are not what we need to immediately consider. What is really important is how many keys we can have. Consider the sizes of key spaces for some ciphers studied early in this text.

  • Monoalphabetic Cipher: |Key Space| \(= 26!\approx 4\times10^{26}\)
  • Vigenère's Cipher using only English words for keys: |Key Space| \(\approx 470,000\)
  • Falconer's Transposition with 4 letter keys: |Key Space|= \(16,777,216=2^{4!}\)

While these numbers are large they hardly compare to the size of the plaintext or ciphertext spaces. Even if we restrict ourselves to counting the number of five character messages there are already \(26^5=11,881,376\) possibilities; sentences of length 30 would bring that up to \(26^{30}\approx 3\cdot 10^{42}\text{.}\)

Definition 5.2.25. Perfect Secrecy.

An encryption system has perfect secrecy if having a piece of ciphertext gives no information about the plaintext. That is with a randomly chosen key a plaintext message is equally likely to be enciphered as any possible ciphertext.

Comprehension Check

Suppose that you intercepted the message ZZZZZZ which you happen to know was enciphered using the modern Vigenère table (figure Figure C.0.8).

  • What would the plaintext be if the key were ZGGZXP?
  • What would the plaintext be if the key were WVUVMW?
  • What would the plaintext be if the key were KRAAZH?
  • Could you find a key so that ZZZZZZ represents the plaintext “thirty”?
  • Could you find a key so that ZZZZZZ represents the plaintext “purple”?
  • Could you find a key so that ZZZZZZ represents any six character plaintext that you like?
  • How do you think these observations relate to the definition of perfect secrecy (definition Definition 5.2.25)?

Suppose we want to encipher a message using a Vigenère cipher, but we encipher six characters at a time and each block is enciphered using a randomly chosen six letter key. In this situation we would have

  • |Plaintext Space|=|all possible six character combinations|=\(26^6=308,915,776\)
  • |Key Space|=|all possible six character combinations|=\(26^6=308,915,776\)
  • |Ciphertext Space|=|all possible six character combinations|=\(26^6=308,915,776\)
Remark 5.2.28.

It should be noted that the security of Vernam's cipher relies on being able to generate truly random sequences (a currently unsolved problem in computer science) and being able to keep the keys synchronized and secret. With advances in quantum computing technology these are becoming more likely, but realizing/implementing truly perfect secrecy remains difficult at best.

Finally, make sure that you have paid close attention to the idea of combining strings with the exclusive or. This is a topic we will return to later when we consider Feistel cipher's and the Data Encryption Standard.

Figure 5.2.29. ITA2/Vernam Cipher Cell