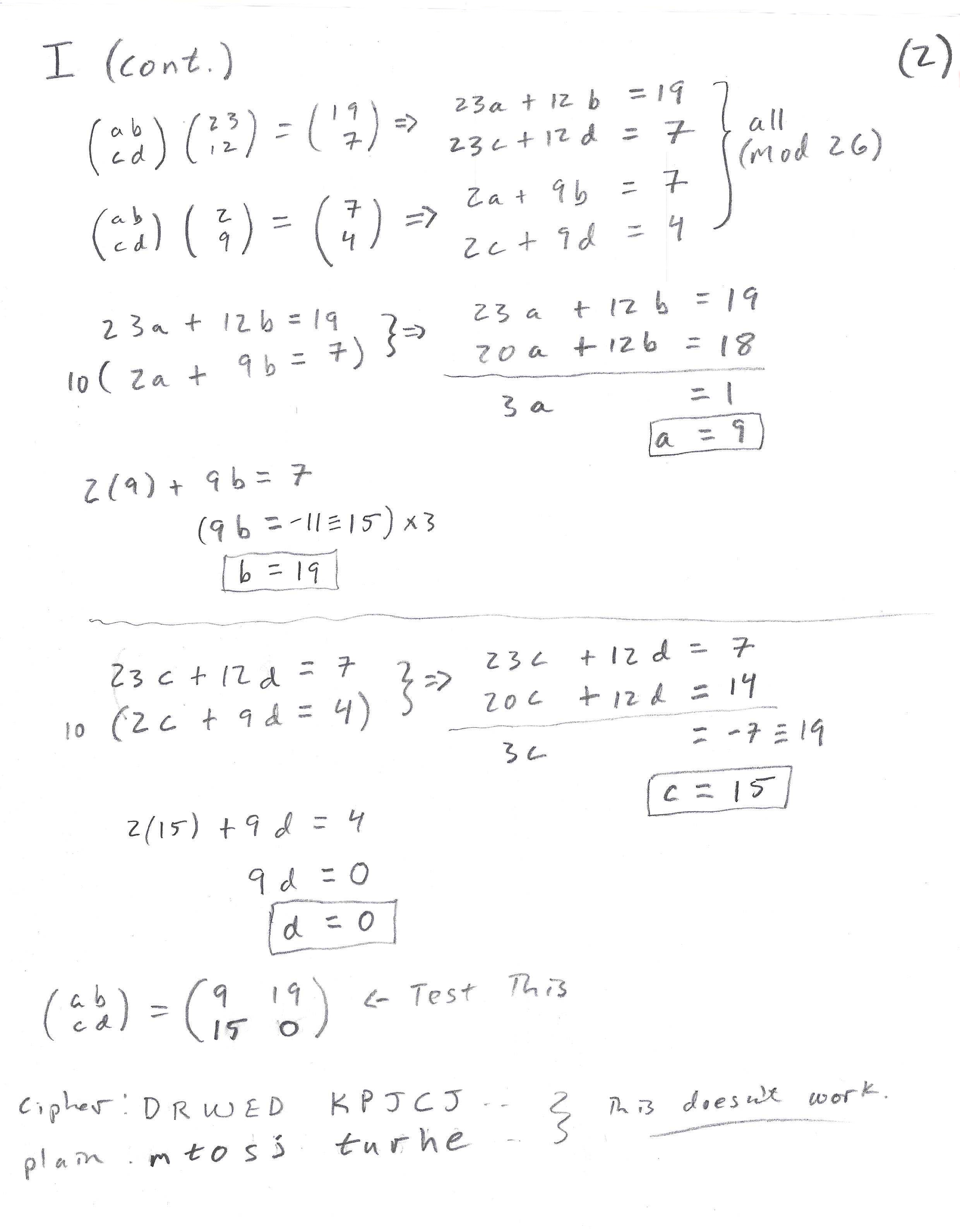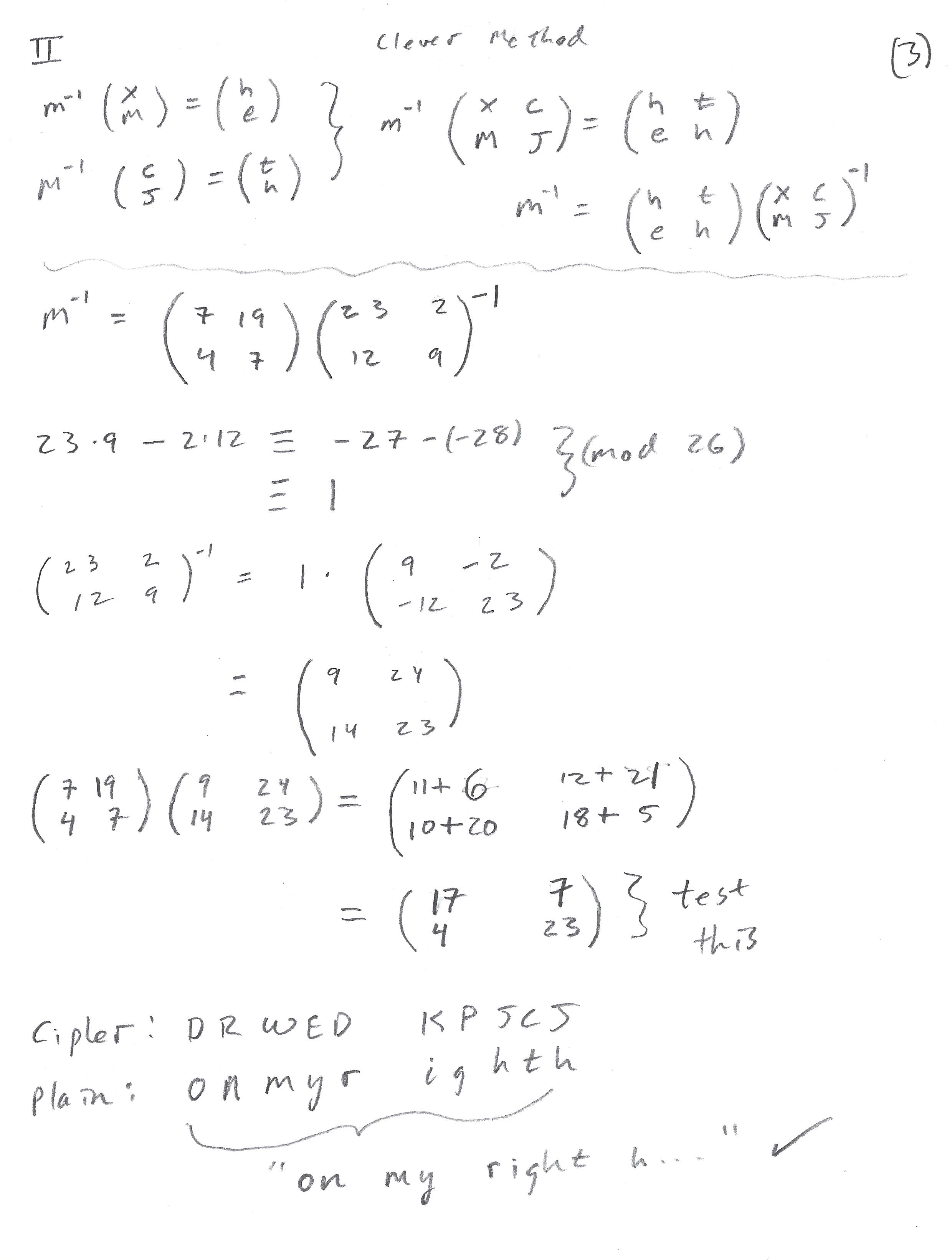Hill's Cipher Analysis (Ciphertext Only)

Section E.4 Hill's Cipher Analysis (Ciphertext Only)

Suppose that we are gievn the following cipher text:

DRWED KPJCJ NNMBX MBAQU BALMP KWQYN UMZWD CFJSM 
IWBAE ERFLM DCGEQ YHIDK ACYAQ YHIES MFZVL APLMG 
PSHRD ERFKA REBSI WLTAE LBBAX MJGFP JCLTB VXVPN 
UMSCH WSJXM DIKWL TZXUV RJMYZ VTOZF IWNNX EZQJE 
ZXWGV SJXWG HZHJN NDIPK SFFBD XBNPM WQMGH WKWMB 
DKFOZ XTOZF BNMGA NOUMU PKZUC JGMCJ BNZDD ISJXM 
EWMQW TFBCJ BNKGW GHWGO FLZXF AKWKL HJBVD PSCNA 
LNPXW GCJOA WCAEH XYJMQ DTZUC JLLVJ FYHVA CNEWD 
PXBAR UBPPF YAYEU IFJLT HVMWJ GZXFJ DRKGZ VDYZU 
QUVWN NQVBO YUPYE IIWVC NGBEJ QVPJM JSDRY APFLT 
HJRQI WMQCJ DPBVE EQLBO IQHRW QLMFS MKJSG NNNFS 
FYCZH RTHBV LMTZL LOUWE REPFD XZDCJ PFZQY UZXLM 
PJORT MNLXM QUFJB NLTOE VPZFD RIWES TTUXS IBVPY 
LRCJD PNNEK DPHRR TBVHI XGZWD THIGN WQPUR ULBBN 
ISWXF PJCDK UNJCN NHCXM RUPWM DHRWE XMVBZ UFYGY 
BFPXJ SDCRT NNISD PCJPF YELVM YSNVB LIFJJ CSJEI 
NNDTF BHRAC BETHP FXMDE DKCUR ZXMFJ ZQOIY RLMPK 
ZXCJV JHSBE PYBAV GLTHR ZUCJI WFYCZ IWMQH RUIZU 
HRUIS ECJBF BNREJ XNNTK TEPXG YXEBO EEPKY ALTDR 
LLDXL LHROP KAWBZ VWDTM BXVCQ LCZKM VPLWC FXMZD 
...

Looking at the character frequencies we can see that this is not a monoalphabetic or transposition cipher. A little more playing around with frequencies of subsets, or looking for evenly spaced repeated strings, reveals that it is probably not a Vigenère cipher either. Let's try to see if it was enciphered with a Hill's Cipher.

The length of your message is 1720 characters

Rank	N-Gram	Count	Percent
1.	J	102	5.93
2.	M	94	5.465
3.	N	90	5.233
4.	X	87	5.058
5.	B	84	4.884
6.	P	76	4.419
7.	C	76	4.419
8.	W	74	4.302
9.	I	72	4.186
10.	L	71	4.128

The length of your message is 1720 characters

Rank	N-Gram	Count	Percent
1.	XM	36	2.093
2.	CJ	30	1.744
3.	NN	22	1.279
4.	LT	20	1.163
5.	SJ	17	0.9884
6.	PX	16	0.9302
7.	BN	16	0.9302
8.	IW	15	0.8721
9.	ZX	14	0.814
10.	JX	14	0.814

Since a basic Hill's cipher encrypts two characters at a time we will focus on bigrams. The most common bigrams in the ciphertext are XM and CJ, one of these probably represents ‘th’ and the other is likely ‘he’. The first possibility we will test is:

\begin{equation*} m\begin{pmatrix} t \\ h\end{pmatrix}=\begin{pmatrix} X \\ M\end{pmatrix}\ \text{and}\ m\begin{pmatrix} h \\ e\end{pmatrix}=\begin{pmatrix} C \\ J\end{pmatrix}. \end{equation*}

where \(m\) is the matrix used to encipher the text. Converting the letters to numbers this gives:

\begin{equation*} m\begin{pmatrix} 19 \\ 7\end{pmatrix}=\begin{pmatrix} 23 \\ 12\end{pmatrix}\ \text{and}\ m\begin{pmatrix} 7 \\ 4\end{pmatrix}=\begin{pmatrix} 2 \\ 9\end{pmatrix}. \end{equation*}

Which further simplifies to:

\begin{equation*} m^{-1}\begin{pmatrix} 23 \\ 12\end{pmatrix}=\begin{pmatrix} 19 \\ 7\end{pmatrix}\ \text{and}\ m^{-1}\begin{pmatrix} 2 \\ 9\end{pmatrix}=\begin{pmatrix} 7 \\ 4\end{pmatrix}. \end{equation*}

If we write

\begin{equation*} m^{-1}=\begin{pmatrix}a & b\\ c & d\end{pmatrix} \end{equation*}

then these equations give us four equations and four unknowns:

\begin{align*} 23a+12b & \equiv 19&\pmod{26}\\ 2a+9b & \equiv 7&\pmod{26} \end{align*}

\begin{align*} 23c+12d & \equiv 7&\pmod{26}\\ 2c+9d & \equiv 4&\pmod{26} \end{align*}

If we solve these equations we get \(a=9\text{,}\) \(b=19\text{,}\) \(c=15\text{,}\) and \(d=0\text{,}\) that is

\begin{equation*} m^{-1}=\begin{pmatrix}9 & 19\\ 15 & 0\end{pmatrix}. \end{equation*}

Using the Hill's Cipher app in Appendix B we get the output:

CIPHER: DRWED KPJCJ...
plain: mtosj turhe...

This means our first attempt was not successful. Let's try the second possibility listed above.

The second pairing of bigrams will give us:

\begin{equation*} m\begin{pmatrix} t \\ h\end{pmatrix}=\begin{pmatrix} C \\ J\end{pmatrix}\ \text{and}\ m\begin{pmatrix} h \\ e\end{pmatrix}=\begin{pmatrix} X \\ M\end{pmatrix}, \end{equation*}

or in numbers

\begin{equation*} m\begin{pmatrix} 19 \\ 7\end{pmatrix}=\begin{pmatrix} 2 \\ 9\end{pmatrix}\ \text{and}\ m\begin{pmatrix} 7 \\ 4\end{pmatrix}=\begin{pmatrix} 23 \\ 12\end{pmatrix}. \end{equation*}

This time however we can try being a little more clever by noting that we can combine these to get:

\begin{equation*} m\begin{pmatrix} 7 & 19\\ 4 & 7\end{pmatrix}=\begin{pmatrix} 23 & 2\\ 12 & 9 \end{pmatrix}. \end{equation*}

We can use this to find \(m^{-1}\) with matrix multiplication and inverses instead of systems of equations:

\begin{align*} m^{-1} &= \begin{pmatrix} 7 & 19\\ 4 & 7\end{pmatrix}\begin{pmatrix} 23 & 2\\ 12 & 9 \end{pmatrix}^{-1}\\ &= \begin{pmatrix} 7 & 19\\ 4 & 7\end{pmatrix}(1)\begin{pmatrix} 9 & -2\\ -12 & 23 \end{pmatrix}\\ &= \begin{pmatrix} 7 & 19\\ 4 & 7\end{pmatrix}\begin{pmatrix} 9 & 24\\ 14 & 23 \end{pmatrix}\\ &= \begin{pmatrix} 17 & 7\\ 4 & 23\end{pmatrix}. \end{align*}

Again, using the Hill's Cipher app in Appendix B we get the output:

CIPHER: DRWED KPJCJ...
plain: onmyr ighth...

This means that our plaintext seems to start with “On my right ...”, and so we have found the correct key. Deciphering the entire original quote points to the following text:

“On my right hand there were lines of fishing stakes resembling a mysterious system of half-submerged bamboo fences, incomprehensible in its division of the domain of tropical fishes, and crazy of aspect as if abandoned forever by some nomad tribe of fishermen now gone to the other end of the ocean; for there was no sign of human habitation as far as the eye could reach. To the left a group of barren islets, suggesting ruins of stone walls, towers, and blockhouses, had its foundations set in a blue sea that itself looked solid, so still and stable did it lie below my feet; even the track of light from the westering sun shone smoothly, without that animated glitter which tells of an imperceptible ripple. And when I turned my head to take a parting glance at the tug which had just left us anchored outside the bar, I saw the straight line of the flat shore joined to the stable sea, edge to edge, with a perfect and unmarked closeness, in one leveled floor half brown, half blue under the ...” -The Secret Sharer By Joseph Conrad

Below are copies of the scrap hand work that went into finding the key for this cipher. Notice that things don't always work perfectly the first time, this doesn't mean that they won't work at all, it might just take some additional attempts.